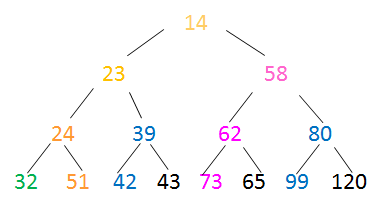
顶堆
小顶堆
小顶堆(Min-Heap)是一种特殊的完全二叉树,它满足以下特性:
- 结构性质:小顶堆是一个完全二叉树,这意味着除了最后一层外,其他所有层都是完全填满的,并且最后一层的所有节点都是尽可能地靠左排列。
- 堆序性质:在小顶堆中,任何一个父节点的值都小于或等于它的子节点的值。这意味着堆的根节点(即顶部)是所有节点中的最小值。
以下是小顶堆的一些基本操作:
- 插入:当我们向小顶堆中插入一个新的节点时,为了维持堆的性质,可能需要进行一系列的上浮操作。具体来说,如果一个节点比它的父节点小,那么它就与父节点交换位置。这个过程会一直持续,直到该节点不再比它的父节点小或者它已经成为了根节点。
删除最小值:由于堆的根节点是最小值,所以删除最小值的操作就是删除根节点。然后,我们将堆的最后一个节点移到根的位置,然后进行一系列的下沉操作来恢复堆的性质。具体来说,一个节点如果比它的子节点大,那么它就与值最小的子节点交换位置。这个过程会一直持续,直到该节点不再比它的子节点大或者它已经成为了叶子节点。 - 建堆:给定一个数组,我们可以通过一系列的操作将其转化为一个小顶堆。常用的方法是“自底向上”的建堆方法。
小顶堆在很多算法和数据结构中都有应用,例如优先队列、Dijkstra's算法等。
大顶堆
大顶堆(Max-Heap)是一种特殊的完全二叉树,它满足以下特性:
- 结构性质:大顶堆是一个完全二叉树,这意味着除了最后一层外,其他所有层都是完全填满的,并且最后一层的所有节点都是尽可能地靠左排列。
- 堆序性质:在大顶堆中,任何一个父节点的值都大于或等于它的子节点的值。这意味着堆的根节点(即顶部)是所有节点中的最大值。
例题
问题:已知小顶堆:{51,32,73,23,42,62,99,14,24,39,43,58,65,80,120},请问62对应节点的左子节点是73.
-
小顶堆:每个非叶子结点的关键值都<其孩子节点的关键值
-
按照完全二叉树将数字填入
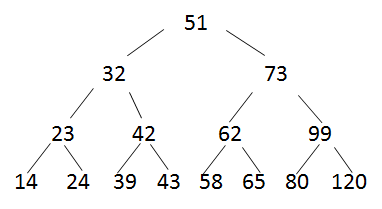
-
再从最后一个非叶子结点开始调整,选孩子结点中小的那个
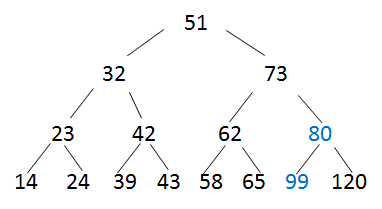
-
对第3层都做如上调整
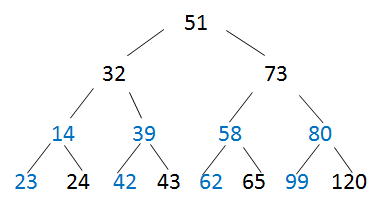
-
对第3个结点调整时,需要一直比较到叶子结点
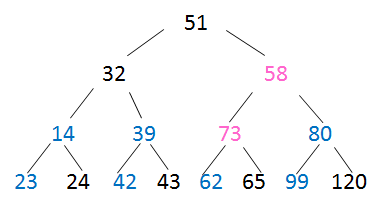
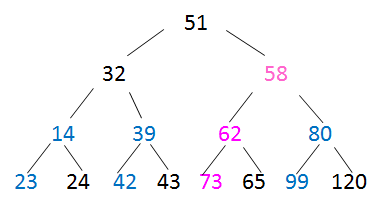
-
调整第2个结点:
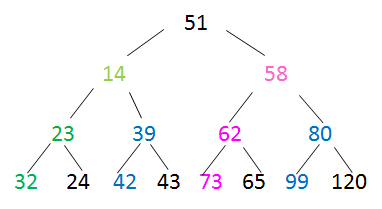
-
最后调整根结点,得到小顶堆为: